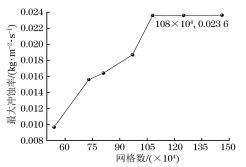
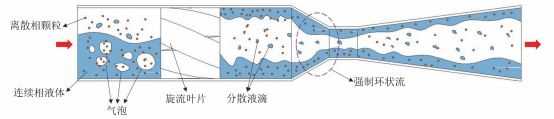
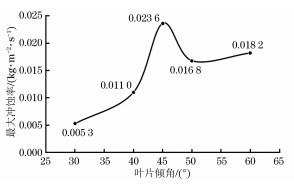
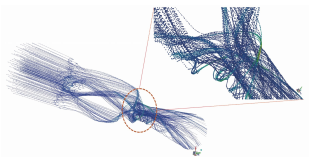
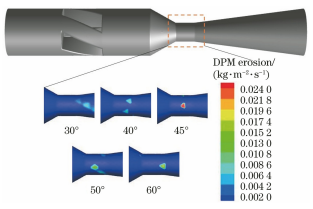
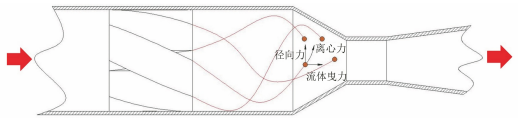
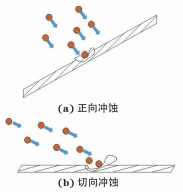
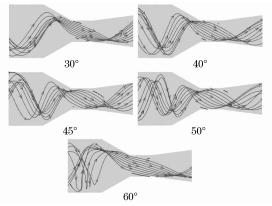
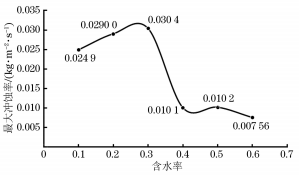
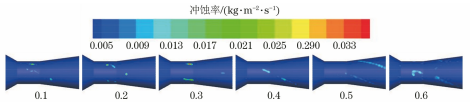
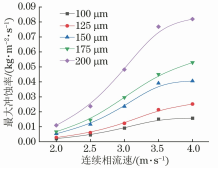
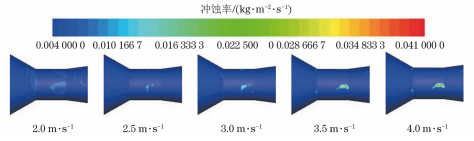
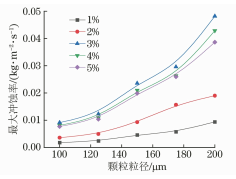
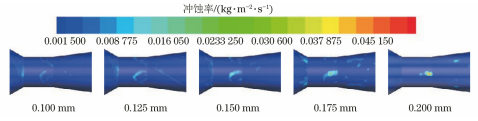
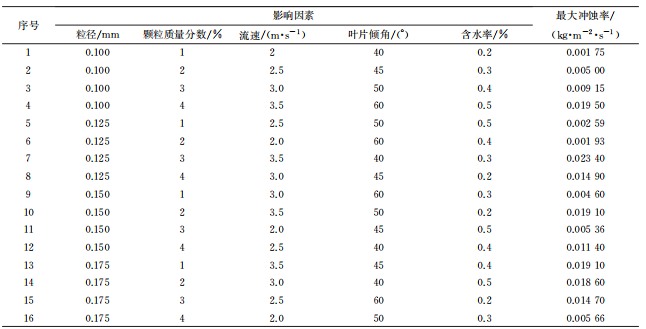
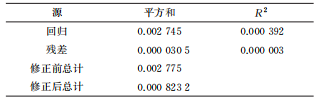
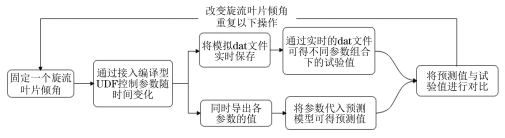
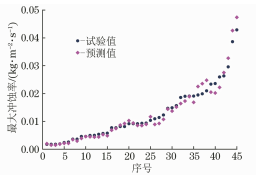
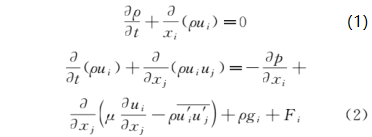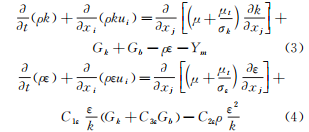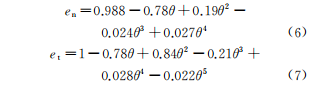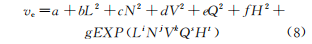在流体输送系统中过流部件通常容易受到输送颗粒的侵蚀作用，长期冲刷腐蚀会对部件的壁面造成不可逆的损伤甚至导致其失效。带涡流的文丘里管在实际工程中应用于多个领域，如分离、航空 、流量计量、气泡发生器、燃烧等，现有研究多集中于对水平管或者弯管等的冲蚀研究，对带涡流或是强制环状流的文丘里管的冲蚀研究较少，因此笔者结合工程应用场景中带强制环状流的文丘里管的实际情况，研究了强制环状流文丘里管的冲刷腐蚀影响。

应用欧拉方法对流场建模，其中，质量和动量守恒方程见式(1)和(2)

式中：ρ为流体密度；u为流体速度；p为压力；μ为动态黏度；g为重力加速度；Fi为离散相作用于连续相的附加源项，i和j是1到3的整数。

需要指出，在本研究中，雷诺应力项ρu_i^'u_j^'是通过标准k-e模型来解释的，其中湍流动能和耗散率见式(3)和(4)

式中：G_k和G_b分别表示平均速度梯度和浮力的湍流动能，Y_m是可压缩湍流中的波动膨胀对总耗散率的贡献，μ_t表示湍流黏度，C_1ε， C_2ε，C_2ε，σ_k和σ_ε是常数。

在本研究中，拉格朗日方法被应用于DPM粒子追踪。基于牛顿第二定律，粒子运动的追踪方程可以表示为：

离散相颗粒与壁面的相互作用可以表示为如下形式 :

式中：e_n和e_t分别为法向恢复速度和切向恢复速度，θ为入射角。

采用CFD-DEM流固耦合数值计算方法，多相流模型采用 VOF模型，湍流模型采用标准k-e模型；入口设置为速度入口，出口设置为压力出口；出入口DPM类型为escape、壁面为reflect；连续相为methane和water-liquid；离散相固体颗粒为圆球状，材料类型为石英砂，密度为2650 kg/m³；壁面材料类型为steel，粗糙高度为0.1mm，粗糙度常数为0.5。

3. 1  模型主要结构

旋流叶片共4片，长25mm，高10mm，α角为叶片倾角；文丘里主要结构参数如下：入口内径30mm，β为收缩段收缩角，喉部直径12mm，喉部长12mm，渐扩段渐扩角7.43°，模型总长187mm，α角设为30°，40°，45°，50°，60°，β角设置为45°。模型主要结构及尺寸见图1。

图 1  模型主要结构及参数

3.2   网格剖分及无关性验证

采用ICEM软件对模型进行完全结构化网格 剖分,平均单元网格质量为 0. 887，最小正交质量为0.82。 网格结构如图 2所示。

图 2   网格剖分示意

网格密度对流场计算结果至关重要，网格越少模拟精度越低，但是网格过密会增加计算时间且计算机的性能要求也会相应增加。因此进行网格独立性验证很有必要。在网格独立性验证过程中,分析了7组网格数量(54×10⁴、73×10⁴、81×10⁴、97×10⁴、 108×10⁴、125×10⁴、146×10⁴) 下的最大冲蚀率。各网格数量下的最大冲蚀率如图3所示，可以看出，当网格数从108×10⁴增加到146×10⁴时,计算结果 变化不明显,但计算效率降低。 因此,为了获得合适 的精度和较高的计算效率,选择网格数108×10⁴。

图3 网格无关性的验证结果

4. 1   叶片倾角对冲刷腐蚀的影响

在水平管中流体常呈现气泡流、段塞流、分层流等流形,而固体颗粒主要分布于液体中,少量颗粒被气体卷携或被液滴带起。通过叶片的旋流作用,气液两相形成气芯-液膜的强制环状流, 由于离心作用重质固体颗粒大部分被甩至靠近壁面的液膜中,只有少量颗粒浮于气相或液滴中,强制环状流示意图见图 4。

图 4   强制环状流示意

叶片倾角会影响强制环状流的旋流出流角度及流体与壁面的切向角度,在工程应用中旋流叶片倾角各不相同,旋流叶片倾角常设计为30°~60°，在此 倾角区间内形成的环状流效果最好。因此，为了更好研究叶片倾角对文丘里管冲刷腐蚀的影响，采用叶片倾角α为 30°、40°、45°、50°、60°，文丘里管收缩段收缩角β为 45°，连续相流速为3m/s，入口含水率为0.2，离散相颗粒质量流量为0.06kg/s，颗粒粒径为150μm，图5为不同叶片倾角下文丘里管的最大冲蚀率曲线。

图 5  不同叶片倾角下文丘里管的最大冲蚀率

由图5可知，文丘里管最大冲蚀率与旋流叶片倾角呈现一定的指数关系。当旋流叶片倾角小于45°时，冲蚀率随着倾角的增大而增大；当旋流叶片倾角大于45°时，随着倾角的增大冲蚀率总体呈现下降趋势，当叶片倾角 45°时，冲蚀率出现极大值，为2.36×10^-2 kg/(m² ·s)。图6为粒子运动轨迹图，由于叶片的旋流作用粒子呈现螺旋状，多条旋臂在缩管附近汇合，可知缩管附近冲蚀最为严重。图7为不同叶片倾角下，文丘里管冲蚀率云图，可知冲蚀主要集中在收缩管附近，且冲蚀强度随着叶片倾角的增大先增大后减小，当叶片倾角为45°时冲刷腐蚀最严重。这是因为，离散相颗粒受到离心力、径向力、流体曳力等因素的影响，其中，离心力使固体颗粒产生切向运动，径向力使得颗粒沿径向运动，曳力维持颗粒和流体运动方向一致，颗粒受力分析见图8，其中离心力造成颗粒对壁面的切向冲蚀，流体曳力致使颗粒与壁面产生正向冲蚀，径向力使得颗粒离开壁面，冲蚀方向示意见图9，当旋流叶片倾角较小时，叶片对流体的轴向加速效果较好，离心切向加速效果较弱，颗粒对壁面的正向冲蚀较强，切向冲蚀较弱，总体冲蚀情况不严重。随着叶片倾角增大，叶片对流体的轴向加速效果减弱，而离心切向加 速效果增强,颗粒切向冲蚀逐渐加剧，总体冲蚀强度增大，在倾角45°时正向冲蚀与切向冲蚀的总和达到最大值。叶片倾角进一步增大切向冲蚀占主导地位，正向冲蚀减弱明显,整体冲蚀效果减弱。流体流线反映了管内的流场动态分布，流体流线图见图10，可知随着旋流叶片倾角的增大流体旋流螺旋的螺距逐渐缩短，切向冲蚀加剧。

图6 颗粒运动轨迹图

图 7  不同叶片倾角下的文丘里管冲蚀率云图

图 8  颗粒受力分析

图 9  正向冲蚀与切向冲蚀

图10 流体流线图

4. 2  含水率对冲刷腐蚀的影响

含水率对固体颗粒冲蚀有着直接影响，为研究含水率对文丘里管冲刷腐蚀的影响规律，设置含水率为0.1、0.2、0.3、0.4、0.5、0.6,旋流叶片倾角为45°，连续相流速为3m/s，离散相颗粒质量流量为0.06kg/s，颗粒粒径为150μm。图11为不同含水率下文丘里管的最大冲蚀率曲线。可以看出，最大冲蚀率随含水率的增大先略有增大后迅速减小，最后基本不变。由图12可知，冲蚀率先增大后减小，且当含水率0.3时为最大，冲蚀位置逐渐从缩管处后移至扩张段。这是因为，在强制环状流中，液膜受到壁面黏性阻力的影响，流速低于气芯，在含水率较小时气相对颗粒的运动起着主导作用，因此含水率较小时颗粒运动更加剧烈，冲蚀相对更严重。而当含水率低于某一值时，随着含水率的增大，液膜加厚，更多的颗粒被液膜拖曳至壁面附近，冲蚀略有增强，当含水率为0.3时，冲蚀率达到极大值，为3.04×10^-2kg/(m²·s) 。含水率大于某一值时冲蚀率先大幅下降后基本不变，这是因为当含水率达到一定值，液膜对颗粒的拖曳作用已经达到极限，更厚的液膜也无法增大对颗粒的束缚作用。

图11 不同含水率下的最大冲蚀率

图12 不同含水率下的冲蚀率云图

4.3  流速对冲刷腐蚀的影响

针对叶片倾角45°、收缩角度45°的文丘里管进行模拟，由图13可见，冲蚀率随着连续相流速的增大而增大。

图13 不同颗粒粒径下，连续相流速对最大冲蚀率的影响

图14为含水率0.2，粒径150μm、颗粒质量分数3%时，叶片倾角45°、收缩角度45°的文丘里管在5种不同流速下的最大冲蚀率分布云图，可以看出冲刷腐蚀依次增大，且冲刷腐蚀面积也逐渐扩大，即随着流速的增大，冲刷腐蚀越来越严重。其冲蚀机理为：当流速增大时，气液固三相流体受到的离心作用增强，且液体对离散相颗粒的曳力增大，颗粒的动能也就随之增大。

图14 不同流速下的冲蚀率云图

4.4  颗粒粒径对冲刷腐蚀的影响

离散相颗粒粒径对强制环状流下的文丘里管冲刷腐蚀有着重要影响，由图15可以看出最大冲蚀率随着颗粒粒径的增大而增大且基本呈现线性变化，而不同颗粒质量分数下冲蚀率的变化趋势不同，从纵向来看，冲蚀率随着颗粒质量分数的增大先增大后减小。

图15 不同颗粒质量分数下颗粒粒径对冲蚀率的影响规律

图16为含水率0.2，流速3m/s，颗粒质量分数3%，叶片倾角45°、收缩角度45°的文丘里管在5种粒径下的最大冲蚀率分布云图，可以看出随着颗粒粒径的增大，冲蚀率逐渐增大，且冲刷腐蚀面积也逐渐扩大，即随着颗粒粒径的增大，冲刷腐蚀加剧。其原因是，随着颗粒粒径增大，颗粒所受惯性增加，且颗粒粒径更大意味着更大的表面受力面积，在离心力、流体曳力、径向力及惯性的共同作用下颗粒对壁面的冲刷腐蚀加剧。

图16 不同颗粒粒径下的冲蚀率云图

4.5   回归分析

在以上研究的基础上,为进一步探讨各因素之间的相关度、多重共线性，同时建立基于强制环状流的文丘里管冲蚀率预测模型，采用专业数据分析软件Matlab和多元回归模型(模型为二次多元方程与指数方程的平均值)，分析叶片倾角、含水率、颗粒粒径、浓度以及流速对冲刷腐蚀的影响，并建立回归方程，正交试验设计及结果见表1。

表1 正交设计及结果

基于多元非线性回归方法，建立最大冲蚀率 (DPM Erosion) 预测模型：

式中：ve为最大冲蚀率；a、b、c、d、e、f、g、i、j、k、s、t均为常数；L为离散相颗粒粒径；N为颗粒质量分数；V为流速；Q为旋流叶片倾角；H为含水率；回归模型参数值见表2。

表2 回归模型参数

对模型进行方差分析，如表3所示，可知回归模型的R²为0.963，回归效果理想。

表3 方差分析结果

为验证模型精度，从五个影响因素中随机选择若干个参数组合进行试验，试验时首先固定一个叶片倾角，然后通过接入编译型 UDF，控制其他4种因素在一定范围内随时间随机变化(每 2×10⁴时间步变化一次，确保每一工况都计算收敛)，试验中将模拟过程进行实时保存，且导出各参数的值，将各参数代入预测模型可得预测值，流程见图17。最后将试验结果与预测值进行比较，图18为试验值与预测值对比图，图中将冲蚀率进行升序排列。

图17 试验验证流程

由图18可知，试验值与预测值较为接近，说明回归模型预测精度较高，即上述最大冲蚀率预测模型可用于强制环状流的文丘里管的冲刷腐蚀预测。

图18 试验值与预测值对比图

作者：

钟  浩^1,2,3，张兴凯^1,2,3，廖锐全^1,2,3

工作单位：

1.  油气钻采工程湖北省重点实验室(长江大学)

2.  长江大学石油工程学院

3.  中国石油天然气集团公司气举试验基地多相流研究室

来源：《腐蚀与防护》2025年4期